最近，bat365正版官方网站量子功能材料设计与应用实验室姚裕贵教授研究组（刘铖铖博士、周金健博士生、姚裕贵教授）和德州大学达拉斯分校的张帆博士合作提出了弱拓扑绝缘体和复合的外尔(Weyl)半金属可以在一类动力学稳定和业已合成的范德瓦尔斯(van der Waals)材料－beta-Bi₄X₄(X=Br,I)中实现。相关研究成果发表在近期的《物理学评论快报》上（Phys. Rev. Lett. 116, 066801 (2016)）。该工作得到了校基础基金以及国家自然科学基金委和科技部的资助。

     以拓扑绝缘体为代表的一系列量子态的发现正在革新并深化了我们对量子材料的基本认识。这种基本认识和理解可能导致前所未有的技术应用优势。比如，拓扑绝缘体中可控的量子相变以及受保护的自旋动量锁定的表面态在Majorana基的拓扑量子计算中有着重要的应用前景。三维的拓扑绝缘体需要用四个拓扑指标来描述 (v0; v1,v2,v3)。如果v0不等于0，即为所谓的强拓扑绝缘体；如果 v0＝0，而 v1,v2,v3 不全为零，则称为弱拓扑绝缘体。强拓扑绝缘体具有奇数个Dirac表面态，而弱拓扑绝缘体具有偶数个Dirac表面态。值得指出的是，强、弱拓扑绝缘体是一同被理论首先预言出来的。很快，实验上便证实和发现了若干个强拓扑绝缘体材料。该类拓扑绝缘体被研究的最多也最透彻。这得益于大多数的强拓扑绝缘体都是层状材料。该结构特点使得实验上可以很容易在解理面上观察到强拓扑绝缘体的指纹－奇数个表面Dirac锥，而不需要特别的表面钝化处理。然而，令人惊讶的是，到目前为止实验上还没有发现弱拓扑绝缘体。一个自然的想法是通过堆垛二维的拓扑绝缘体来得到弱拓扑绝缘体。该方法的最大问题是弱拓扑绝缘体的特征表面Dirac锥只能在侧面而非解理面观察到，而在其解理面（平行于堆垛平面）没有特征表面态。我们知道非解理面难于获得且不稳定，同时会具有大量的悬挂键，这些都给实验验证带来了巨大的挑战。因此，找到一个新的体系能够在实验上易于验证且能够便于研究弱拓扑绝缘体特有的新奇物性是迫切和重要的。

       在前期研究该类二维大能隙拓扑绝缘体的工作基础上（Nano Lett. 14， 4767 (2014)），最近，bat365正版官方网站量子功能材料设计与应用实验室刘铖铖博士、周金健博士生、姚裕贵教授和德州大学达拉斯分校的张帆博士合作提出了弱拓扑绝缘体可以在范德瓦尔斯(van der Waals)材料－beta-Bi₄X₄(X=Br,I)中实现并可以容易地被实验验证。如图1所示，该类材料的基本构建单元是一维的原子链。垂直于该原子链方向的两个晶面(100)和(001)都是解理面。本征的beta-Bi₄Br₄、beta-Bi₄I₄分别是弱拓扑绝缘体和强拓扑绝缘体。他们还发现单轴应变可以使得体系发生拓扑相变。在不同的应变区，可以得到强拓扑绝缘体、弱拓扑绝缘体以及普通的能带绝缘体，如图3所示。对于弱拓扑绝缘体，在(001) 解理面是没有拓扑表面态的，而在(100) 解理面，出现了两个各向异性的表面Dirac锥，见图2。并且，当对该体系进行电荷掺杂时，可以发现该表面态发生了四次Lifshitz转变。alpha-Bi₄Br₄、alpha-Bi₄I₄由于其元胞沿c方向长度加倍，相应的高对称点都反带两次，所以都是拓扑平庸的能带绝缘体。值得特别指出的是，如图4所示，在从弱拓扑绝缘体到强拓扑绝缘体转变的同时破缺体系的反演对称性，会出现一个全新的Weyl半金属相，即在两个解理面都出现了费米弧(Fermi arc)，但是只在(100) 解理面出现费米环(Fermi circle)，我们称之为复合的Weyl半金属。

作为典型的弱拓扑绝缘体，该类范德瓦尔斯(van der Waals)材料－beta-Bi₄X₄(X=Br,I)为研究很多新颖的物理提供了一个理想的平台。当体系在平均的意义上具有U(1), 时间反演以及平移对称性时，弱拓扑绝缘体对于无序是稳定的。当破缺其中任一对称性，都将会引入相应的新奇物理效应。如螺位错以及台阶等拓扑缺陷的引入会破缺平移对称性将会导致螺旋的边界态。又如磁性的引入可以破缺时间反演对称性会导致量子反常霍尔效应。再如与超导的邻近耦合效应可以破缺U(1)对称性从而导致带有Majorana 零模的拓扑超导体。

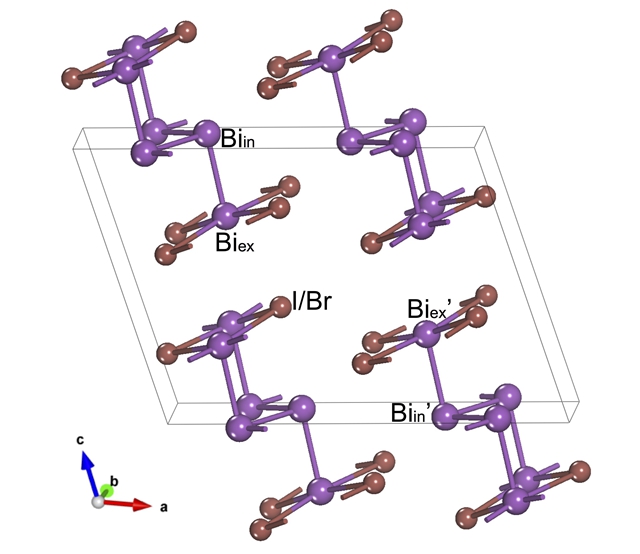
图1 beta-Bi4X4(X=Br,I)的晶体结构。体系关于(010)面具有镜面反演同时具有空间反演对称性。

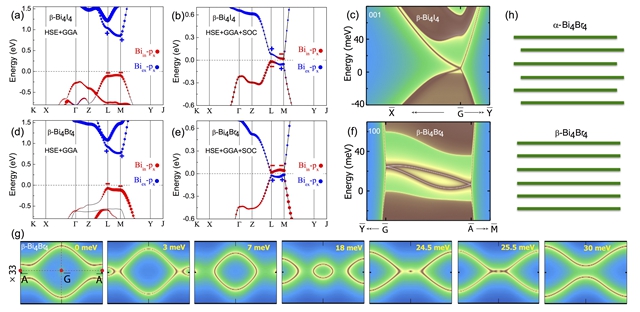
图2 电子结构。(a) (b) beta-Bi₄I₄有/无自旋轨道耦合的能带结构。(c) beta-Bi₄I₄的(001)表面态。(d)(e) beta-Bi₄Br₄有/无自旋轨道耦合的能带结构。(f) beta-Bi₄Br₄的(100)表面态。(g) beta-Bi₄Br₄的(001)表面态的Lifshitz转变。(h) alpha/beta-Bi₄Br₄的堆垛示意图。

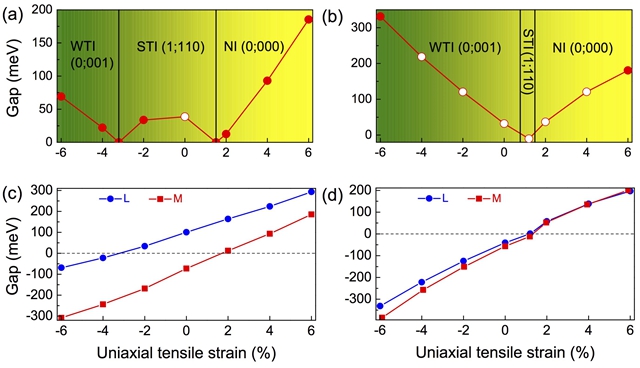
图3 单轴应力导致的beta-Bi4X4(X=Br,I)的拓扑相变。

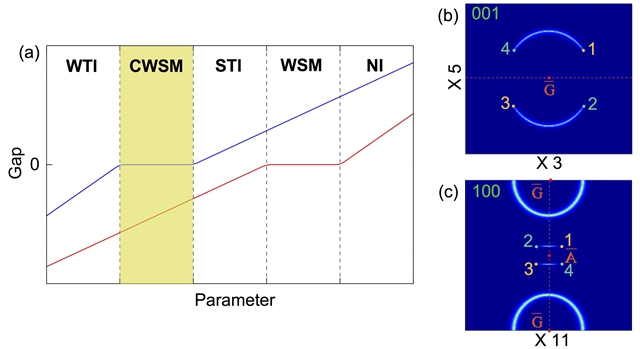
图4 (a) 相图。强弱拓扑绝缘体相变时可出现我们提出的复合Weyl 半金属。而强拓扑绝缘体和能带绝缘体的拓扑相变时可出现通常的Weyl 半金属。(b) 复合Weyl 半金属在(001)解理面的Fermi arc。(c) 复合Weyl 半金属在(100)解理面共存的Fermi arc以及Fermi circle。